The quantum relativistic character of the charge carriers in 2D materials give rise to plethora of exotic effects. Among the most remarkable ones we can find Klein tunneling, atomic collapse, negative refraction, the Hofstadter butterfly, anti-Klein tunneling, cloaked states and non-conventional superconductivity. Most of these effects have been confirmed experimentally. However, others remain elusive such as the Zitterbewegung (ZB) and Hartman effect (HE).
The ZB originally predicted by Schrödinger is the rapid oscillatory motion of relativistic particles.
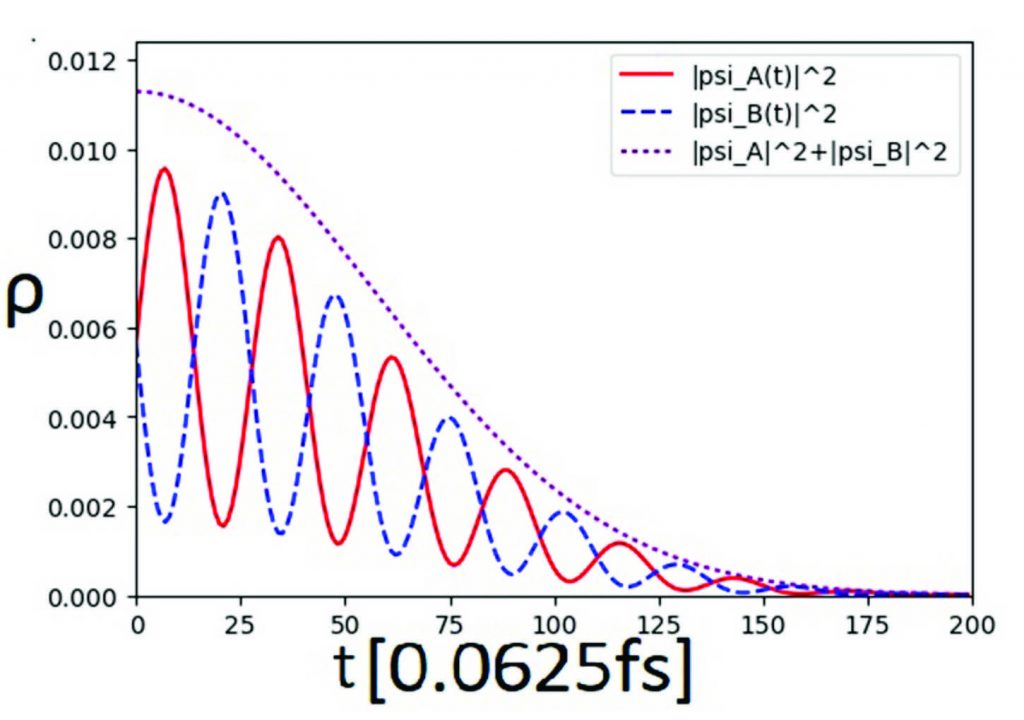
The ZB is caused by the interference between positive and negative energy states in the wave packet.
The frequency of ZB motion is determined by the gap between these two states and the amplitude of oscillations in a particle position is of the order of the Compton wavelength.
The HE is the tunneling effect through a barrier where the tunneling time is independent of the thickness of an opaque barrier. This phenomenon was first described by Thomas E. Hartman in 1962.
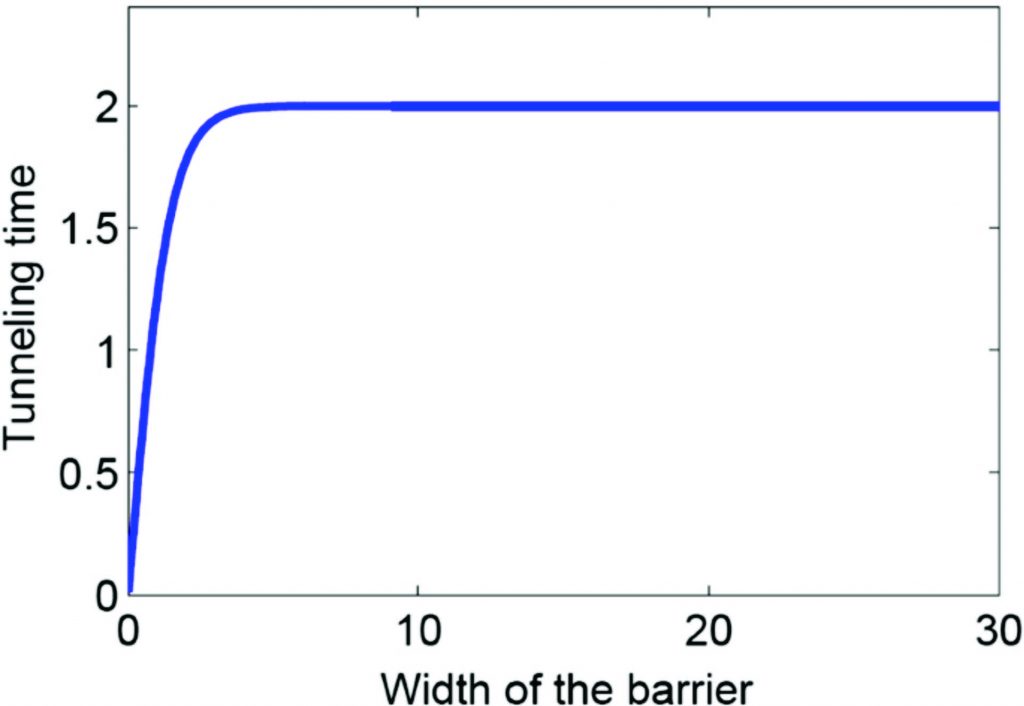
As a tunneling wave phenomenon it can take place in all kind of waves: matter waves, electromagnetic waves and sound waves.
In the 2DMRG we are interested in several exotic phenomena that can take place in 2D materials. Particularly, we are devoted to study ZB, HE, giant conductance, Ramsauer-Townsend effect, cloaked states, Fano resonances, Klein, and anti-Klein tunneling. In the case ZB, we have demonstrated theoretically the existence of pseudospinorial ZB in a quasi-one-dimensional graphene nanoribbon. We have found evidence of trembling antiphase oscillations in the probability density time-distribution for each graphene sublattice state. Interestingly, several features of the PZBE become tunable, even its complete disappearance at the vicinity of the Dirac points or at a symmetric pseudospin configuration. We also have a significant progress in the study of Fano resonances. For details see the section devoted to them. Currently, we are assessing: the ZB in quasi-two-dimensional nanostructures, the tunneling times in single, double, and multiple barriers. We also expect to analyze in the short and middle term the phenomena of giant conductance and Ramsauer-Townsend oscillations.
