When we talk about 2D materials, we are alluding to dimensionality, a parameter that plays an important role as a defining parameter in materials science. The same element can have such different properties if it has a crystalline structure in different dimensionalities. One of the most versatile chemical elements in terms of dimensionality is Carbon. This is presented as Diamond and Graphite in a 3D arrangement, in the form of nanotubes in 1D and in the form of Fullerenes speaking of 0D. The 2D arrangement was one of the paradigms of solid-state physics for the belief that they were impossible to exist due to thermal fluctuations in low-dimensional crystalline networks, in other words, they were thermodynamically unstable.

A great scientific revolution came with the discovery of graphene by Andre Geim’s group, a purely two-dimensional material made up of carbon atoms arranged in a hexagonal lattice one atom thick, approximately 0.15 nm. This discovery was worthy of the Nobel Prize 2010. Graphene presents a series of exotic effects that are due to the behavior of electrons at low energies, which controlled by a linear dispersion relationship similar to the Dirac equation present a mass equal to zero and a speed 300 times less than the speed of light, this causes effects such as Klein tunneling and an anomalous Hall effect, among others. However, graphene has a disadvantage, it does not have an energy bandgap, which makes its direct application to nanoelectronics complicated.
The investigations not only remained in graphene but it has also been analyzed what happens when stacking two or more sheets of graphene. This is how bilayer graphene was obtained, a quasi-2D material, with a distance between layers of approximately 0.35 nm. Bilayer graphene is very similar to graphene, it has excellent electrical and thermal conductivity, it is flexible and highly transparent. Unlike graphene, bilayer graphene at low energies has a parabolic scattering relationship and the electrons now behave as Dirac fermions with mass, this causes exotic effects that are very different from what happened in graphene: Anti-Klein tunneling, an integer quantum Hall effect, cloaking states, and Fano resonances. Bilayer graphene has an advantage over graphene, it is possible to modulate the opening bandgap by applying an external electric field.
Of the exotic effects, one of the most interesting are the Fano resonances,
“an effect that occurs by the superposition of systems with propagating or continuous states and systems with evanescent states, were commonly a light source, a magnetic field, or some other quantity physical play the role of mixing to give rise to the superposition between both states”
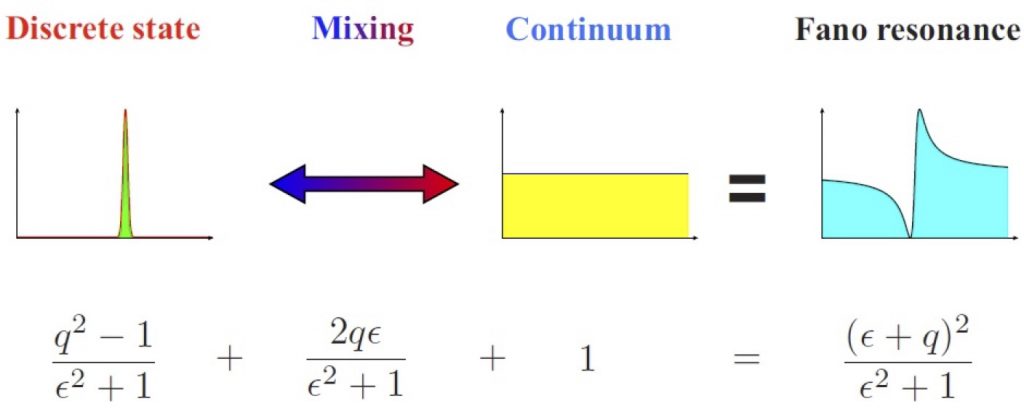
In the 2D MATERIALS RESEARCH GROUP, we have given ourselves the task of investigating the Fano resonances in the bilayer graphene. This phenomenon in bilayer graphene occurs by the coupling between propagating and confined states in electrostatic barriers at oblique incidence.
This gives rise to the typical asymmetrical line shape of these special resonances in the electron transmittance. The Fano profile is quite sensitive to the angle of incidence and Fano resonances can also be shifted readily by changing the structural parameters of the barriers. Furthermore, Fano resonances can leave a hallmark in the transport properties, specifically the conductance.
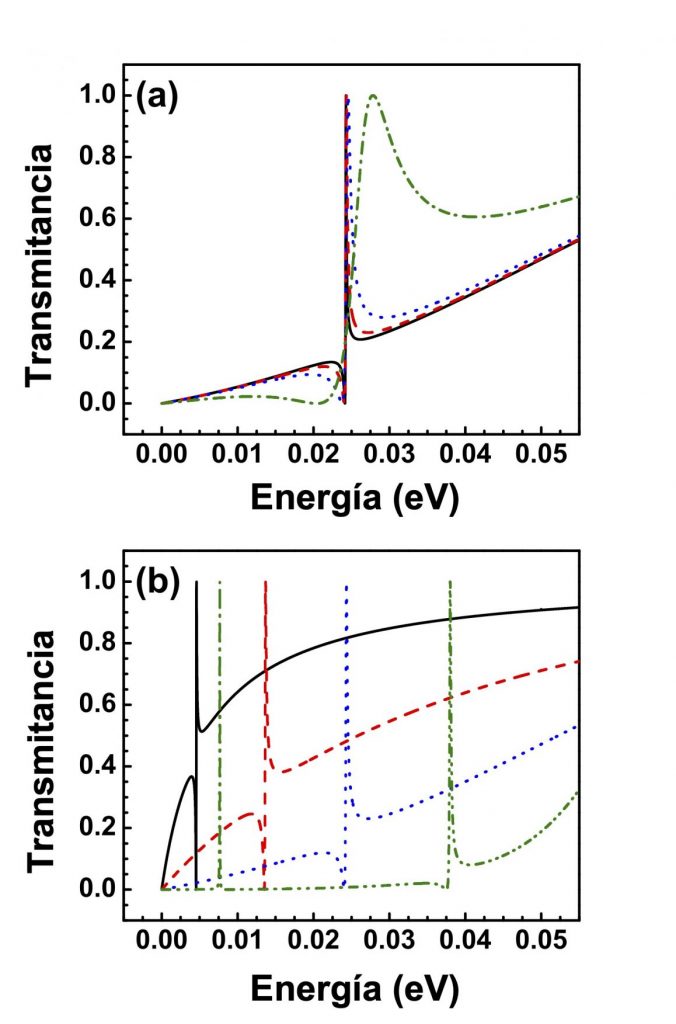
Even more, by reducing the angular range in the computation of the transport properties the conductance curves can manifest a Fano profile. In bilayer graphene double barriers and superlattices the coupling between Fano resonances and resonant (miniband) states gives rise to the so-called hybrid resonances. The contribution of these resonances can be tracked and identified in the conductance curves. Fano resonances can be considered as exotic as anti-Klein tunneling, cloaked states, and unconventional superconductivity because with simple electrostatic barriers we can have them. This is in stark contrast with the typical systems in which Fano resonances arise. With the opening bandgap, we find that the signatures of the Fano resonances on the conductance are enhanced by the opening of the bandgap. In fact, the Fano profile is manifested in the conductance without the need of reducing the angular range. This enhancement results from the improvement of the chirality matching between extended and discrete states induced by the bandgap opening.
Throughout the work we have done, the transfer and hybrid matrix methods have been used, as well as the Landauer-Bütikker and Sturm-Liouville formalisms. We are currently working on how Fano and hybrid resonances can improve thermoelectric properties in heterostructures based on bilayer graphene.