“It is well known that superlattices with non-conventional profiles can serve as stop and pass band filters. “
The Gaussian profile is the archetypal profile that eliminates the undesirable Gibbs oscillations that arise typically in periodic superlattices. However, there are multiple non-conventional profiles, such as Lorentzian, linear, arithmetic, and of Lévy type to mention a few, that can help to improve the characteristic of stop and band pass filters. The concept of non-conventional superlattices is broad and can be used in the propagation of electromagnetic, acoustic, and electron waves. In semiconductor superlattices, the potentiality of these profiles has been assessed theoretically and confirmed experimentally. There is also some progress in the electron filtering in 2D materials, especially in graphene. Non-conventional superlattices can also present anomalous electronic transport and special states.
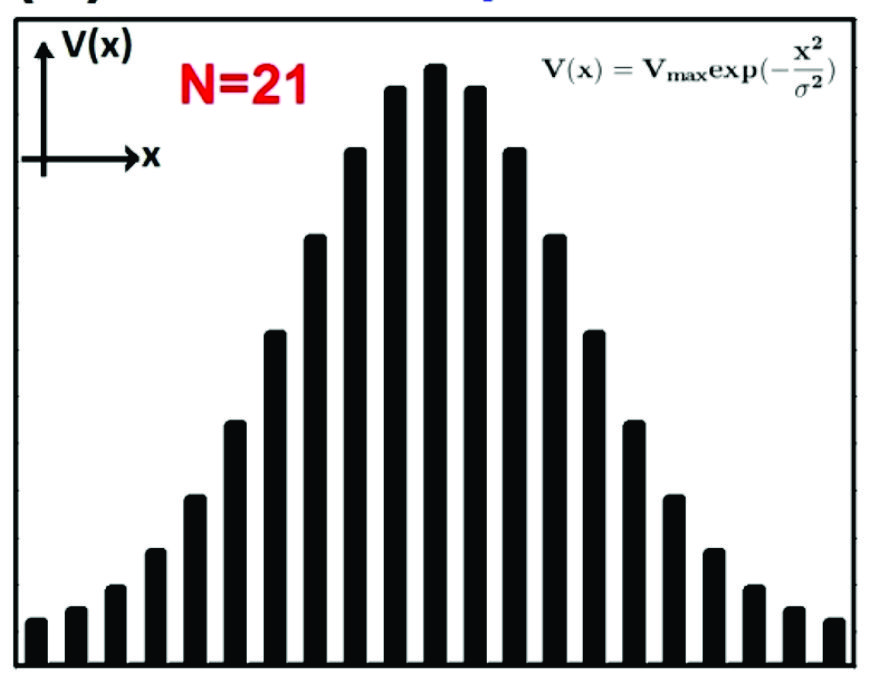
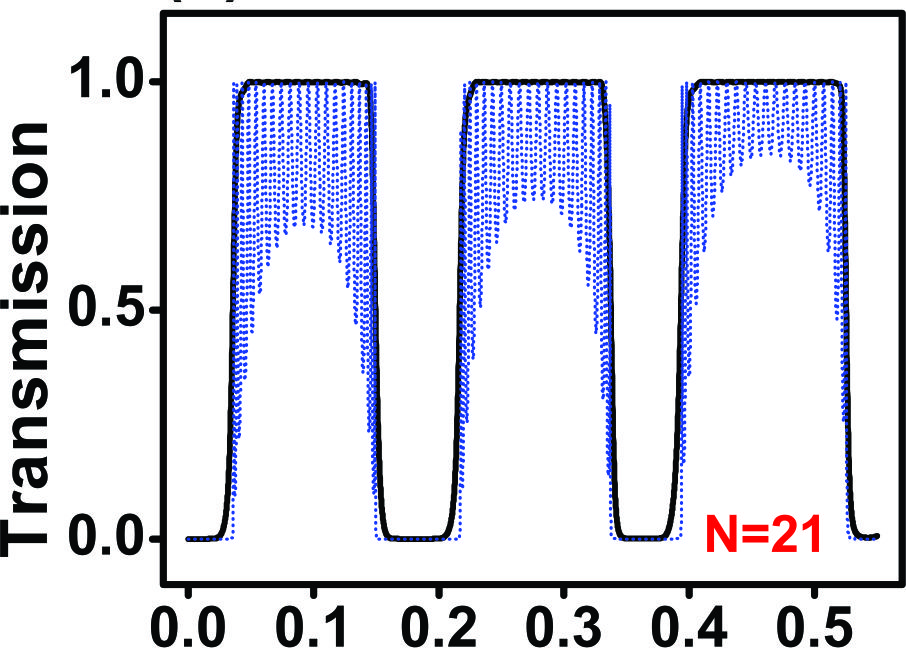
The 2DMRG is exploring the transmission and transport properties of non-conventional superlattices in 2D materials. Potential profiles such as Gaussian, Lorentzian, linear and Pöschl-Teller have been assessed as stop and pass band electronic filters. In particular, the importance of electron states inside the barriers is analyzed. Likewise, the electronic and transport properties of biperiodic graphene superlattices have been studied. Particular attention has been paid to the characteristics of the so-called transparent states. The 2DMRG is also assessing the electronic transport in arithmetic, Gaussian and Lévy type Fermi velocity graphene superlattices. In this case the special distribution of Fermi velocity barriers give rise to anomalous electronic transport. The aim of the 2DMRG is to extent these studies to other 2D materials as well as to exploit the special characteristics of non-conventional superlattices to improve the spin-valley polarization, magnetoresistive and thermoelectric properties.
